Notes of ML Study for CNN Equivalence

Math derivation for a CNN problem

Let’s consider the CNN operation:

\[\begin{aligned} \sum_j f_1(x) =& \sum_j \alpha_j A_j(x,x_j) := \sum_j \alpha_j A_j \\ \sum_j f_2(x) =& \sum_j \beta_j B_j(x,x_j) := \sum_j \beta_j B_j \\ &\dots \end{aligned}\]

Given intuition by:

\[\begin{aligned} \alpha_1 A_1 \beta_1 B_1 &= \alpha_1 A_1 \cdot \beta_1 B_1\\ \alpha_1 A_1 \beta_1 B_1 + \alpha_2 A_2 \beta_2 B_2 &\neq (\alpha_1 A_1+\alpha_2 A_2) \cdot (\beta_1 B_1+\beta_2 B_2) \\ but &= \\ \frac{1}{2}(\alpha_1 A_1+\alpha_2 A_2) \cdot (\beta_1 B_1+\beta_2 B_2) &+\frac{1}{2}(\alpha_1 A_1-\alpha_2 A_2) \cdot (\beta_1 B_1-\beta_2 B_2), \end{aligned}\]

a more general equality is to be derived.

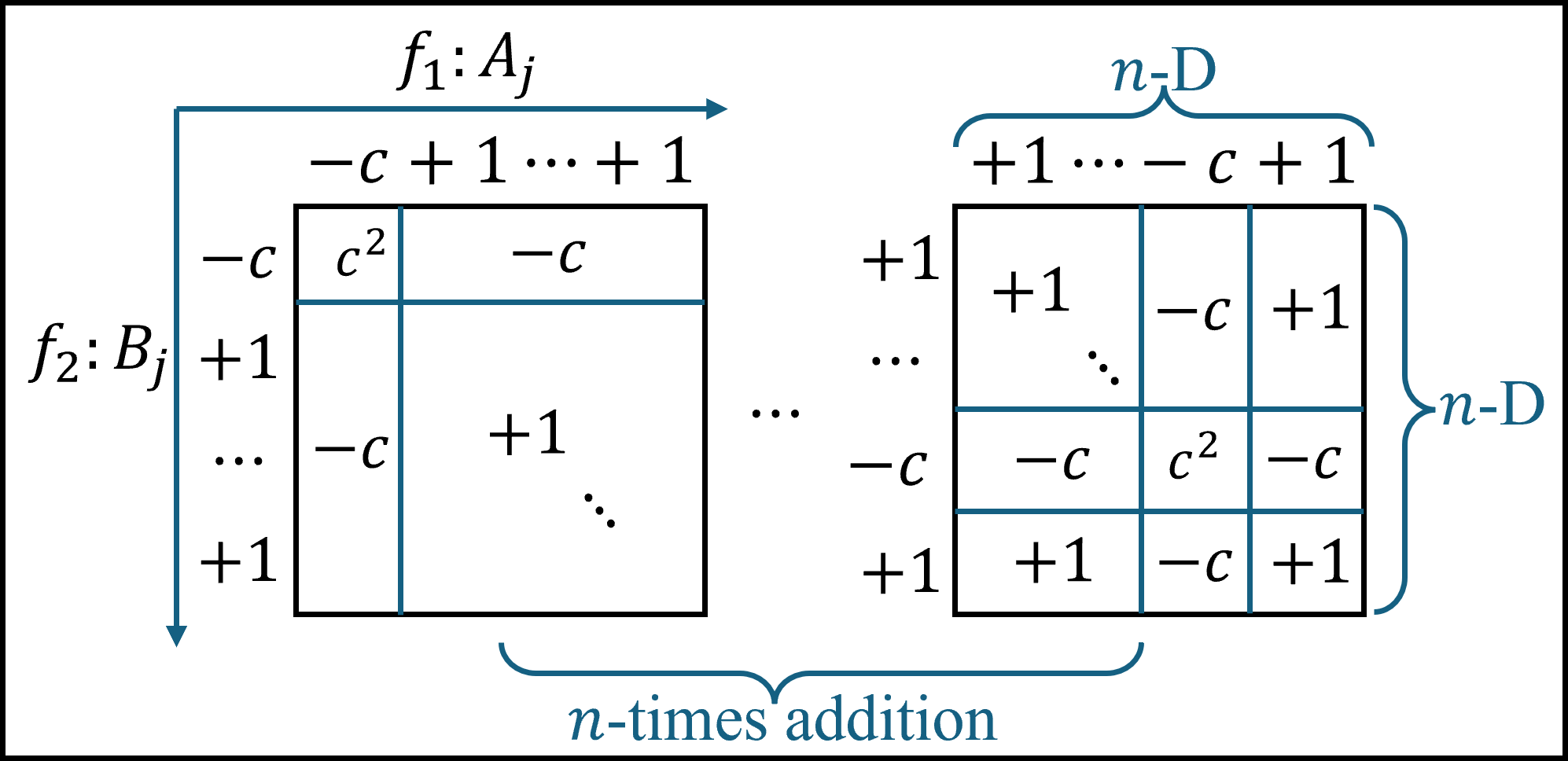
As illustrated in the figure, the desired \(\textbf{diagonal}\) product addition \(\sum_{j=1}^n A_j B_j\) can be realized by alternating extra signs and weights. Normally, every combination unit \(A_p B_q\) is added \(n\) times which results in \(n\)-times magnitudes. However, every combination has two chances to change its sign, when each dimension (\(A\) or \(B\)) alters the negative sign to index \(p\) or \(q\). Thus, there are only \(n-2\) times simple addition and twice negative-sign additions. We further let \(c=\frac{n-2}{2}\) be the weight when the addition sign is negative, so the final result for all non-diagonal addition is guaranteed 0. For diagonal terms, nonetheless, the net addition gives \((c^2+n-1)A_j B_j\). It should then be normalized by this amount.

Therefore, we can formulate:

\[\sum_{j=1}^n f_1(x) f_2(x) = \frac{1}{(\frac{n-2}{2})^2+n-1} \sum_{k=1}^n (C_k \circ F_1 )(x) \cdot (C_k \circ F_2 )(x),\]

where $C_k$ is the kernel representation of aforementioned sign-weight alternation. It is acted on basic CNN kernels $F_1$ and $F_2$, where originally:

\[F_1(x) = \sum_j f_1(x),~ and ~ F_2(x) = \sum_j f_2(x)\]